Data无损压缩

研究问题&动机

传统的data deduplication是对整个数据块进行去重，而去重需要两个数据块完全相同，才能认为有相同的base。但对于time series data（论文中举的例子是传感器检测温度的数据）来说，相邻的数据块可能会非常相似，但是因为不是完全相同，所以没有办法去重（现有的研究也有提出一种multi-step的方法，即当出现第一个重复的chunk，除了去重之外，还要遍历一遍查找相似的chunk，再进行delta compression）。因此提出的压缩算法适合压缩相似但不完全相同的时序数据。

通用的基于LZ的压缩算法不适合大规模数据，因为他们的窗口比较小，并且没有办法考虑全局的数据。因此在这种基础上，为大规模数据提出了data deduplication的概念。

压缩算法

整个压缩的主要逻辑就是要将chunk分成两部分，一部分是basis（用于deduplication），另一部分是deviation（直接存储不进行压缩）。

如果选择deviation的长度为2个字节，那么可以对2^16 = 65536个相似的数据块进行去重。

假设一共有c个chunk，不妨分别记为z₁, z₂,…,z_c。并且每一个chunk的长度都是n比特。压缩算法会把每一个chunk z_i分割成两个部分，一个是长度为k的base x_i，另一个是长度为m的deviation y_i。

但是在压缩之前会先进行一个移位的操作，因为在time series data中，通常会有一些bits跟其余部分的关联性很低（比如LSB的数据很难根据MSB的数据进行推测，这两个关联性不大）。想要实现的是尽可能的分成两个关联性低的部分。

为了定量的精确衡量这种关联性的大小，使用两个随机变量的互信息来定义：

$$I(x,y) = H(x) + H(Y) - H(X, Y)$$

如果假设deviation的长度m是已知的，J是对应deviation的下标集合，那么移位的操作希望最小化H(Z_J, Z_J^C)的互信息取值。

当chunk很大的时候，一一枚举开销非常大，使用贪心算法进行m次迭代：

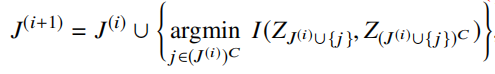
（或者也可以设置停止条件，但是可能迭代次数会更多？）

这样的压缩算法可以保证稳定性（某些chunk损坏不会影响剩下其他chunk的压缩和解压）和对数据的即时存储、搜索和查找。

重点：估计过程只需要用training set做一次！可以开始的时候系统先不压缩，收集一定量的数据完成估计过程，确定J的下标集合

因为还需要解压，所以还需要对J进行存储。因为J中的内容是m个取值范围不会超过n的整数，所以可以用Elias gamma code进行编码。这样编码之后需要的空间不会超过$m(2logn+1)$。

压缩过程需要一个deduplication dictionary（初始是一个空词典），用来存储已经出现过的base。

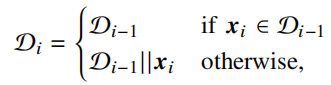
如果已经出现，换成对应id+deviation。

压缩性能

结论

这个压缩算法的最明显的好处是每一个chunk只需要一次pass就可以压缩完成，并且需要移位的下标信息可以预训练获得，可以使用多次。